Class 9 Science Chapter 8: Motion.

Table of Contents

Chapter 8: Motion – Short Notes

1. Introduction

An object is said to be in motion if its position changes with time with respect to a fixed reference point (origin).
Rest: An object is said to be at rest if its position does not change with time with respect to its surroundings.

2. Scalar and Vector Quantities

Scalar Quantity: A physical quantity that has only magnitude (size). Example: Distance, Speed, Mass, Time.
Vector Quantity: A physical quantity that has both magnitude and direction. Example: Displacement, Velocity, Force, Acceleration.

3. Distance and Displacement

Distance: The total path length covered by an object. It is a scalar quantity. (SI unit: metre, m)
Displacement: The shortest straight-line distance between the initial and final position of an object. It has direction. It is a vector quantity. (SI unit: metre, m)
Key Difference: Distance is always positive or zero, while displacement can be positive, negative, or zero.

4. Uniform and Non-Uniform Motion

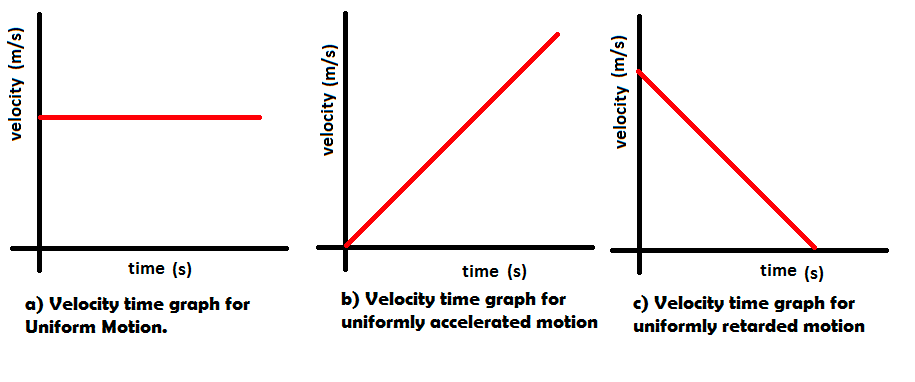
Uniform Motion: When an object covers equal distances in equal intervals of time, however small the time interval may be.
Non-Uniform Motion: When an object covers unequal distances in equal intervals of time.

5. Speed

The distance travelled by an object per unit time.
- Formula: Speed (v) = Total distance travelled (s) / Total time taken (t)
- SI Unit: metre/second (m/s)
Average Speed: Total distance travelled divided by the total time taken.
- Average Speed = Total Distance / Total Time
Uniform Speed: When an object covers equal distances in equal intervals of time.
Variable Speed: When an object covers unequal distances in equal intervals of time.

6. Velocity

The speed of an object in a given direction. It is the displacement per unit time.
- Formula: Velocity (v) = Displacement (s) / Time taken (t)
- SI Unit: metre/second (m/s)
- It is a vector quantity.
Uniform Velocity: When an object undergoes equal displacement in equal intervals of time. (Both magnitude and direction of velocity remain constant).
Average Velocity: Total displacement divided by the total time taken.
- Average Velocity = Total Displacement / Total Time

7. Acceleration

The rate of change of velocity with time.
- Formula: Acceleration (a) = Change in velocity (Δv) / Time taken (t) = (Final velocity - Initial velocity) / Time
- SI Unit: metre/second² (m/s²)
- It is a vector quantity.
Positive Acceleration: Velocity increases with time.
Negative Acceleration (Retardation/Deceleration): Velocity decreases with time.
Uniform Acceleration: When velocity changes by equal amounts in equal intervals of time.

8. Graphical Representation of Motion

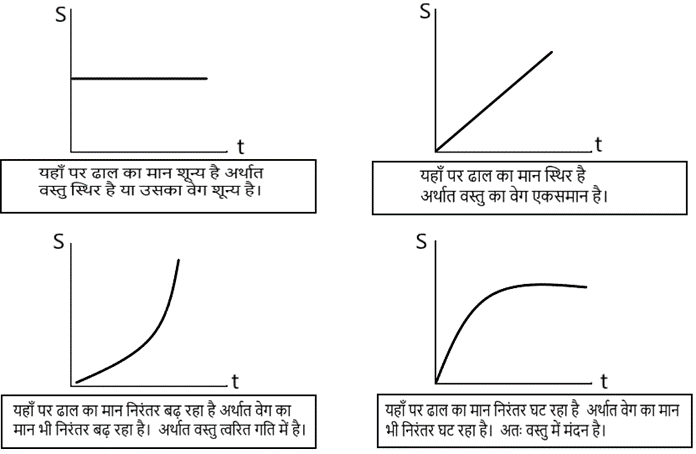
A. Distance-Time Graph

For Uniform Speed: A straight line graph. The slope gives the speed of the object.
- Speed = Slope = (Change in distance) / (Change in time)
For Non-Uniform Speed: A curved graph. The slope at any point gives the speed at that instant.

B. Velocity-Time Graph

For Uniform Acceleration: A straight line graph. The slope gives the acceleration of the object.
- Acceleration = Slope = (Change in velocity) / (Change in time)
The area under the velocity-time graph gives the displacement of the object.

9. Equations of Motion by Graphical Method

For an object moving with uniform acceleration (a), along a straight line with initial velocity (u), final velocity (v), and displacement (s) in time (t).

First Equation of Motion: v = u + at
(Relates velocity and time)
Second Equation of Motion: s = ut + ½at²
(Relates displacement and time)
Third Equation of Motion: v² = u² + 2as
(Relates velocity and displacement)

Where:

v = final velocity
u = initial velocity
a = acceleration
s = distance/displacement
t = time

10. Uniform Circular Motion

When an object moves in a circular path with constant speed.
Key Point: The speed is constant, but the velocity is not constant because the direction of motion changes continuously. Therefore, it is an accelerated motion.
The acceleration is directed towards the centre of the circle (centripetal acceleration).

Important Questions & Answers

Very Short Answer Type Questions (1 Mark)

1. Define displacement.
Ans: Displacement is the shortest straight-line distance between the initial and final position of an object. It is a vector quantity.

2. What is the SI unit of acceleration?
Ans: metre per second squared (m/s²).

3. What does the slope of a distance-time graph indicate?
Ans: The slope of a distance-time graph indicates the speed of the object.

4. When is the acceleration taken as negative?
Ans: Acceleration is taken as negative when the velocity of an object decreases with time. It is also called retardation or deceleration.

5. What remains constant in uniform circular motion?
Ans: Speed remains constant in uniform circular motion.

6. Is displacement a scalar or a vector quantity?
Ans: Displacement is a vector quantity.

7. What is the acceleration of a body moving with uniform velocity?
Ans: Zero. Since there is no change in velocity, acceleration is zero.

Short Answer Type Questions (2-3 Marks)

1. Differentiate between distance and displacement.
Ans:

Distance	Displacement
It is the total path length covered.	It is the shortest straight-line distance between initial and final points.
It is a scalar quantity.	It is a vector quantity.
It is always positive.	It can be positive, negative, or zero.

2. A train starting from a railway station and moving with uniform acceleration attains a speed of 20 m/s in 10 seconds. Find its acceleration.
Ans:

Initial velocity, u = 0 m/s (since it starts from rest)
Final velocity, v = 20 m/s
Time, t = 10 s
Acceleration, a = (v – u)/t = (20 – 0)/10 = 2 m/s²

3. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
Ans: If the distance-time graph is a straight line parallel to the time axis, it means that the distance of the object is not changing with time. Therefore, the object is at rest.

4. A bus decreases its speed from 72 km/h to 36 km/h in 10 seconds. Calculate the acceleration of the bus.
Ans:

First, convert speeds to m/s.
- Initial velocity, u = 72 km/h = 72 × (5/18) = 20 m/s
- Final velocity, v = 36 km/h = 36 × (5/18) = 10 m/s
Time, t = 10 s
Acceleration, a = (v – u)/t = (10 – 20)/10 = (-10)/10 = -1 m/s² (Negative sign indicates retardation).

5. Draw a velocity-time graph for an object moving with uniform acceleration.
Ans: (Draw a straight line graph sloping upwards from the origin. The x-axis is time (t), the y-axis is velocity (v).)

Long Answer Type Questions (5 Marks)

1. a) Derive the first equation of motion (v = u + at) by graphical method.
b) A car starting from rest moves with a uniform acceleration of 0.2 m/s² for 3 minutes. Find the speed acquired and the distance travelled.
Ans:
a) Derivation of v = u + at:

Consider the velocity-time graph for an object moving with uniform acceleration ‘a’.
Let initial velocity at time t=0 be ‘u’ (point A) and final velocity at time t be ‘v’ (point B).
The slope of the graph gives acceleration: a = (BC)/(AC) = (v - u)/t
Rearranging the equation: a = (v - u)/t => at = v - u
Therefore, v = u + at

b) Solution:

Given: u = 0 m/s (rest), a = 0.2 m/s², t = 3 minutes = 3 × 60 = 180 seconds.
Speed acquired (v): Using v = u + at
v = 0 + (0.2 × 180) = 36 m/s
Distance travelled (s): Using s = ut + ½at²
s = (0 × 180) + (½ × 0.2 × (180)²)
s = 0 + (½ × 0.2 × 32400) = (0.1 × 32400) = 3240 metres

2. a) What is uniform circular motion? Why is it called accelerated motion?
b) Study the velocity-time graph of an object given below and find:
(i) The acceleration in the first 4 seconds.
(ii) The retardation in the last 2 seconds.
(iii) The total displacement.
(Assume a graph where velocity increases from 0 to 8 m/s in 4s, remains constant for 2s, then decreases to 0 m/s in 2s)

Ans:
a) Uniform circular motion is the motion of an object in a circular path at a constant speed. It is called accelerated motion because the direction of velocity (which is tangential to the path) changes continuously. Since velocity is a vector quantity, a change in direction constitutes a change in velocity, and therefore, acceleration occurs (centripetal acceleration).

b) Calculations:
(i) Acceleration in first 4 seconds:

Change in velocity, Δv = (8 – 0) = 8 m/s
Time, Δt = 4 s
Acceleration, a = Δv/Δt = 8/4 = 2 m/s²

(ii) Retardation in last 2 seconds:

Change in velocity, Δv = (0 – 8) = -8 m/s
Time, Δt = 2 s
Retardation = -a = – (Δv/Δt) = – (-8/2) = 4 m/s² (or Acceleration = -4 m/s²)

(iii) Total Displacement:

Displacement = Area under the velocity-time graph.
Area 1 (Triangle, 0 to 4s): = ½ × base × height = ½ × 4 × 8 = 16 m
Area 2 (Rectangle, 4 to 6s): = length × breadth = 2 × 8 = 16 m
Area 3 (Triangle, 6 to 8s): = ½ × base × height = ½ × 2 × 8 = 8 m
Total Displacement = 16 + 16 + 8 = 40 metres

3. State the three equations of motion. Derive the second equation of motion (s = ut + ½at²) graphically.
Ans:
The three equations of motion are:

v = u + at
s = ut + ½at²
v² = u² + 2as

Graphical derivation of s = ut + ½at²:

Consider the velocity-time graph for an object moving with uniform acceleration ‘a’.
Let initial velocity be ‘u’ at time t=0 and final velocity be ‘v’ at time ‘t’.
The distance travelled ‘s’ is given by the area under the velocity-time graph.
Area = Area of rectangle OADF + Area of triangle ABD
- Area of rectangle OADF = OA × OF = u × t
- Area of triangle ABD = ½ × base × height = ½ × t × (v – u)
But from first equation, we know (v – u) = at. So, Area of triangle = ½ × t × (at) = ½at²
Therefore, total area (displacement, s) = ut + ½at²
Hence, s = ut + ½at²

Of course. Here is the study material for Class 9 Science Chapter 8: गति in Hindi, perfect for revision.

अध्याय 8: गति – संक्षिप्त नोट्स

1. परिचय

कोई वस्तु गति में कही जाती है यदि समय के साथ उसकी स्थिति एक निश्चित संदर्भ बिंदु (मूल बिंदु) के सापेक्ष बदलती है।
विराम: कोई वस्तु विराम में कही जाती है यदि समय के साथ उसकी स्थिति उसके परिवेश के सापेक्ष नहीं बदलती।

2. अदिश और सदिश राशियाँ

अदिश राशि: वह भौतिक राशि जिसमें केवल परिमाण (मान) होता है। उदाहरण: दूरी, चाल, द्रव्यमान, समय।
सदिश राशि: वह भौतिक राशि जिसमें परिमाण और दिशा दोनों होते हैं। उदाहरण: विस्थापन, वेग, बल, त्वरण।

3. दूरी और विस्थापन

दूरी: किसी वस्तु द्वारा तय किए गए पथ की कुल लंबाई। यह एक अदिश राशि है। (SI मात्रक: मीटर, m)
विस्थापन: किसी वस्तु की प्रारंभिक और अंतिम स्थिति के बीच का सबसे छोटी सरल रेखीय दूरी। इसकी दिशा होती है। यह एक सदिश राशि है। (SI मात्रक: मीटर, m)
मुख्य अंतर: दूरी हमेशा धनात्मक या शून्य होती है, जबकि विस्थापन धनात्मक, ऋणात्मक या शून्य हो सकता है।

4. एकसमान और असमान गति

एकसमान गति: जब कोई वस्तु बराबर समय अंतरालों में बराबर दूरी तय करती है, चाहे समय अंतराल कितना भी छोटा क्यों न हो।
असमान गति: जब कोई वस्तु बराबर समय अंतरालों में असमान दूरी तय करती है।

5. चाल

किसी वस्तु द्वारा एकांक समय में तय की गई दूरी।
- सूत्र: चाल (v) = तय की गई कुल दूरी (s) / लिया गया कुल समय (t)
- SI मात्रक: मीटर/सेकंड (m/s)
औसत चाल: तय की गई कुल दूरी को लिए गए कुल समय से भाग देने पर।
- औसत चाल = कुल दूरी / कुल समय
एकसमान चाल: जब कोई वस्तु बराबर समय अंतरालों में बराबर दूरी तय करती है।
परिवर्ती चाल: जब कोई वस्तु बराबर समय अंतरालों में असमान दूरी तय करती है।

6. वेग

किसी निश्चित दिशा में वस्तु की चाल। यह प्रति एकांक समय में विस्थापन है।
- सूत्र: वेग (v) = विस्थापन (s) / लिया गया समय (t)
- SI मात्रक: मीटर/सेकंड (m/s)
- यह एक सदिश राशि है।
एकसमान वेग: जब कोई वस्तु बराबर समय अंतरालों में बराबर विस्थापन करती है। (वेग का परिमाण और दिशा दोनों नियत रहते हैं)।
औसत वेग: कुल विस्थापन को लिए गए कुल समय से भाग देने पर।
- औसत वेग = कुल विस्थापन / कुल समय

7. त्वरण

समय के साथ वेग में परिवर्तन की दर।
- सूत्र: त्वरण (a) = वेग में परिवर्तन (Δv) / लिया गया समय (t) = (अंतिम वेग - प्रारंभिक वेग) / समय
- SI मात्रक: मीटर/सेकंड² (m/s²)
- यह एक सदिश राशि है।
धनात्मक त्वरण: वेग समय के साथ बढ़ता है।
ऋणात्मक त्वरण (मंदन/अवत्वरण): वेग समय के साथ घटता है।
एकसमान त्वरण: जब वेग बराबर समय अंतरालों में बराबर मात्रा से बदलता है।

8. गति का आरेखीय निरूपण

A. दूरी-समय ग्राफ

एकसमान चाल के लिए: एक सरल रेखा का ग्राफ। ढाल वस्तु की चाल देती है।
- चाल = ढाल = (दूरी में परिवर्तन) / (समय में परिवर्तन)
असमान चाल के लिए: एक वक्रित ग्राफ। किसी भी बिंदु पर ढाल उस क्षण पर तात्क्षणिक चाल देती है।

B. वेग-समय ग्राफ

एकसमान त्वरण के लिए: एक सरल रेखा का ग्राफ। ढाल वस्तु का त्वरण देती है।
- त्वरण = ढाल = (वेग में परिवर्तन) / (समय में परिवर्तन)
वेग-समय ग्राफ के अंतर्गत क्षेत्रफल वस्तु का विस्थापन देता है।

9. आरेखीय विधि द्वारा गति के समीकरण

एकसमान त्वरण (a) से गतिमान एक वस्तु के लिए, जो प्रारंभिक वेग (u) से चलना शुरू करती है, अंतिम वेग (v) प्राप्त करती है, और समय (t) में विस्थापन (s) करती है।

गति का प्रथम समीकरण: v = u + at
(वेग और समय को संबंधित करता है)
गति का द्वितीय समीकरण: s = ut + ½at²
(विस्थापन और समय को संबंधित करता है)
गति का तृतीय समीकरण: v² = u² + 2as
(वेग और विस्थापन को संबंधित करता है)

जहाँ:

v = अंतिम वेग
u = प्रारंभिक वेग
a = त्वरण
s = दूरी/विस्थापन
t = समय

10. एकसमान वृत्तीय गति

जब कोई वस्तु एक वृत्तीय पथ पर नियत चाल से चलती है।
मुख्य बिंदु: चाल नियत होती है, लेकिन वेग नियत नहीं होता क्योंकि गति की दिशा लगातार बदलती रहती है। इसलिए, यह एक त्वरित गति है।
त्वरण वृत्त के केंद्र की ओर निर्देशित होता है (अभिकेंद्रीय त्वरण)।

महत्वपूर्ण प्रश्न एवं उत्तर

अति लघु उत्तरीय प्रश्न (1 अंक)

1. विस्थापन को परिभाषित कीजिए।
उत्तर: विस्थापन किसी वस्तु की प्रारंभिक और अंतिम स्थिति के बीच की सबसे छोटी सरल रेखीय दूरी है। यह एक सदिश राशि है।

2. त्वरण का SI मात्रक क्या है?
उत्तर: मीटर प्रति सेकंड वर्ग (m/s²)।

3. दूरी-समय ग्राफ का ढाल क्या दर्शाता है?
उत्तर: दूरी-समय ग्राफ का ढाल वस्तु की चाल दर्शाता है।

4. त्वरण को कब ऋणात्मक लिया जाता है?
उत्तर: त्वरण को ऋणात्मक तब लिया जाता है जब किसी वस्तु का वेग समय के साथ घटता है। इसे मंदन या अवत्वरण भी कहते हैं।

5. एकसमान वृत्तीय गति में क्या नियत रहता है?
उत्तर: एकसमान वृत्तीय गति में चाल नियत रहती है।

6. विस्थापन एक अदिश राशि है या सदिश?
उत्तर: विस्थापन एक सदिश राशि है।

7. एकसमान वेग से गतिमान पिंड का त्वरण क्या होता है?
उत्तर: शून्य। चूंकि वेग में कोई परिवर्तन नहीं होता, इसलिए त्वरण शून्य होता है।

लघु उत्तरीय प्रश्न (2-3 अंक)

1. दूरी और विस्थापन में अंतर स्पष्ट कीजिए।
उत्तर:

दूरी	विस्थापन
यह तय किए गए पथ की कुल लंबाई है।	यह प्रारंभिक और अंतिम बिंदु के बीच की सबसे छोटी दूरी है।
यह एक अदिश राशि है।	यह एक सदिश राशि है।
यह हमेशा धनात्मक होती है।	यह धनात्मक, ऋणात्मक या शून्य हो सकता है।

2. एक रेलवे स्टेशन से चलना शुरू करने वाली और एकसमान त्वरण से चलने वाली रेलगाड़ी 10 सेकंड में 20 m/s की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए।
उत्तर:

प्रारंभिक वेग, u = 0 m/s (विरामावस्था से)
अंतिम वेग, v = 20 m/s
समय, t = 10 s
त्वरण, a = (v – u)/t = (20 – 0)/10 = 2 m/s²

3. आप किसी वस्तु की गति के बारे में क्या कह सकते हैं जिसका दूरी-समय ग्राफ समय अक्ष के समानांतर एक सरल रेखा है?
उत्तर: यदि दूरी-समय ग्राफ समय अक्ष के समानांतर एक सरल रेखा है, तो इसका मतलब है कि वस्तु की दूरी समय के साथ नहीं बदल रही है। इसलिए, वस्तु विरामावस्था में है।

4. एक बस अपनी चाल 72 km/h से घटाकर 36 km/h कर देती है, इसमें 10 s का समय लगता है। बस का त्वरण ज्ञात कीजिए।
उत्तर:

सबसे पहले, चाल को m/s में बदलें।
- प्रारंभिक वेग, u = 72 km/h = 72 × (5/18) = 20 m/s
- अंतिम वेग, v = 36 km/h = 36 × (5/18) = 10 m/s
समय, t = 10 s
त्वरण, a = (v – u)/t = (10 – 20)/10 = (-10)/10 = -1 m/s² (ऋणात्मक चिह्न मंदन दर्शाता है)।

5. एकसमान त्वरण से गतिमान वस्तु के लिए वेग-समय ग्राफ बनाइए।
उत्तर: (मूल बिंदु से ऊपर की ओर जाती हुई एक सीधी रेखा का ग्राफ बनाएं। x-अक्ष समय (t) और y-अक्ष वेग (v) है।)

दीर्घ उत्तरीय प्रश्न (5 अंक)

1. a) आरेखीय विधि द्वारा गति का प्रथम समीकरण (v = u + at) व्युत्पन्न कीजिए।
b) विरामावस्था से चलना शुरू करने वाली एक कार 0.2 m/s² के एकसमान त्वरण से 3 मिनट तक चलती है। प्राप्त की गई चाल और तय की गई दूरी ज्ञात कीजिए।
उत्तर:
a) v = u + at का व्युत्पत्ति:

एकसमान त्वरण ‘a’ से गतिमान वस्तु के लिए वेग-समय ग्राफ पर विचार कीजिए।
माना समय t=0 पर प्रारंभिक वेग ‘u’ है (बिंदु A) और समय t पर अंतिम वेग ‘v’ है (बिंदु B)।
ग्राफ का ढाल त्वरण देता है: a = (BC)/(AC) = (v - u)/t
समीकरण को पुनर्व्यवस्थित करने पर: a = (v - u)/t => at = v - u
अतः, v = u + at

b) हल:

दिया है: u = 0 m/s (विराम), a = 0.2 m/s², t = 3 मिनट = 3 × 60 = 180 सेकंड।
प्राप्त चाल (v): v = u + at सूत्र का use करने पर
v = 0 + (0.2 × 180) = 36 m/s
तय दूरी (s): s = ut + ½at² सूत्र का use करने पर
s = (0 × 180) + (½ × 0.2 × (180)²)
s = 0 + (½ × 0.2 × 32400) = (0.1 × 32400) = 3240 मीटर

2. a) एकसमान वृत्तीय गति क्या है? इसे त्वरित गति क्यों कहा जाता है?
b) नीचे दिए गए किसी वस्तु के वेग-समय ग्राफ का अध्ययन कीजिए और ज्ञात कीजिए:
(i) पहले 4 सेकंड में त्वरण।
(ii) अंतिम 2 सेकंड में मंदन।
(iii) कुल विस्थापन।
(मान लीजिए एक ग्राफ जहाँ वेग 0 से 8 m/s तक 4s में बढ़ता है, 2s तक स्थिर रहता है, फिर 2s में 0 m/s हो जाता है)

उत्तर:
a) एकसमान वृत्तीय गति किसी वस्तु की एक वृत्तीय पथ पर नियत चाल से होने वाली गति है। इसे त्वरित गति इसलिए कहा जाता है क्योंकि वेग की दिशा (जो पथ के स्पर्शरेखीय होती है) लगातार बदलती रहती है। चूंकि वेग एक सदिश राशि है, दिशा में परिवर्तन वेग में परिवर्तन है, और इसलिए त्वरण होता है (अभिकेंद्रीय त्वरण)।

b) गणना:
(i) पहले 4 सेकंड में त्वरण:

वेग में परिवर्तन, Δv = (8 – 0) = 8 m/s
समय, Δt = 4 s
त्वरण, a = Δv/Δt = 8/4 = 2 m/s²

(ii) अंतिम 2 सेकंड में मंदन:

वेग में परिवर्तन, Δv = (0 – 8) = -8 m/s
समय, Δt = 2 s
मंदन = -a = – (Δv/Δt) = – (-8/2) = 4 m/s² (या त्वरण = -4 m/s²)

(iii) कुल विस्थापन:

विस्थापन = वेग-समय ग्राफ के अंतर्गत क्षेत्रफल।
क्षेत्र 1 (त्रिभुज, 0 से 4s): = ½ × आधार × ऊँचाई = ½ × 4 × 8 = 16 m
क्षेत्र 2 (आयत, 4 से 6s): = लंबाई × चौड़ाई = 2 × 8 = 16 m
क्षेत्र 3 (त्रिभुज, 6 से 8s): = ½ × आधार × ऊँचाई = ½ × 2 × 8 = 8 m
कुल विस्थापन = 16 + 16 + 8 = 40 मीटर

3. गति के तीनों समीकरण लिखिए। गति के दूसरे समीकरण (s = ut + ½at²) को आरेखीय विधि से व्युत्पन्न कीजिए।
उत्तर:
गति के तीन समीकरण हैं:

v = u + at
s = ut + ½at²
v² = u² + 2as

s = ut + ½at² का आरेखीय व्युत्पत्ति:

एकसमान त्वरण ‘a’ से गतिमान वस्तु के वेग-समय ग्राफ पर विचार कीजिए।
माना प्रारंभिक वेग ‘u’ है (समय t=0 पर) और अंतिम वेग ‘v’ है (समय ‘t’ पर)।
तय की गई दूरी ‘s’ वेग-समय ग्राफ के अंतर्गत क्षेत्रफल द्वारा दी जाती है।
क्षेत्रफल = आयत OADF का क्षेत्रफल + त्रिभुज ABD का क्षेत्रफल
- आयत OADF का क्षेत्रफल = OA × OF = u × t
- त्रिभुज ABD का क्षेत्रफल = ½ × आधार × ऊँचाई = ½ × t × (v – u)
परंतु पहले समीकरण से, हम जानते हैं (v – u) = at। अतः, त्रिभुज का क्षेत्रफल = ½ × t × (at) = ½at²
इसलिए, कुल क्षेत्रफल (विस्थापन, s) = ut + ½at²
अतः, s = ut + ½at²

Class 9 Science Chapter 8: Motion.